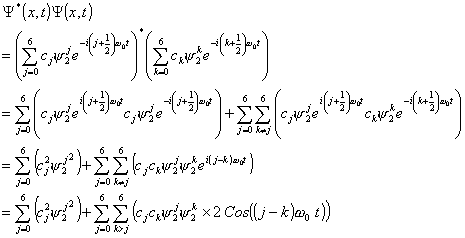Create a web site, where the user can run a simulation of a time-dependant system. The programming will be done in Java.
When the user selects an initial force constant (k1) for the harmonic oscillator, draw the normalized ground state wavefunction. The user should than be able to select a new force constant (k2) using a graphical User Interface (GUI). The program will then compute and draw the second ground state wavefunction, for the new harmonic oscillator.
Using the GUI the user should be able to start the animation that will propagate the
wavefunction in time, drawing it on top of the origional wavefunction until the user clicks on stop.
The following items must be considered in creating a GUI in JAVA;
The internal working of the JAVA program will be to create a canvas,
directly over the GUI, which will be used to display plots of the stationary states of
each wavefunction and display the animation.
In my problem the total time dependant Hamiltonian for a one-dimensional harmonic oscillator system is:

The above Hamiltonian satisfies the time-independent schrodinger equation for times less then zero. If we define the state for times less then zero as state 1 we can find the eigenvalue for a harmonic oscillator using schrodinger equation for a stationary ground state.

And the ground state wavefunction for the system in state 1 is given by:

To evolve the system in time we must find the state of the system when t=0. The state of the system at t=0 can be written as a linear combination of stationary states in state 2. I can write this as:
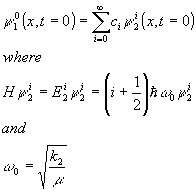
To find the values for the coefficients we need to multiply both sides of the equation by

And, after integrating over all values of x, and using the othonormality condition of state 2, we have
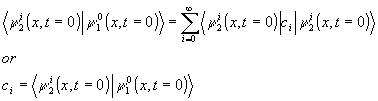
We can now find the coefficients of the equation.
The higher order stationary states (up to the fifth order) for the harmonic oscillator, which are functions related to the Hermite polynomials, are shown in the following equations.
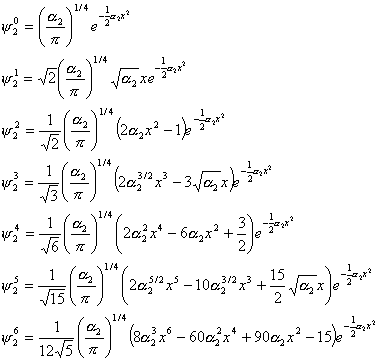
For the problem I have truncated the infinite sum to the 6th term. I can make use of the following integral relationships between odd and even functions in my calculations.
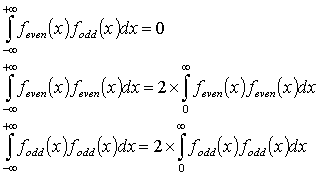
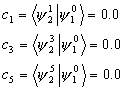
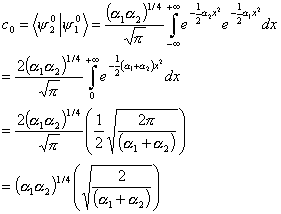
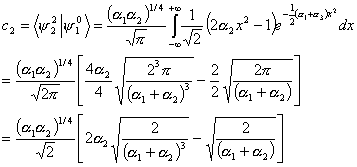
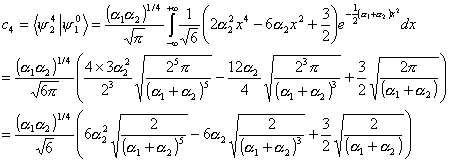
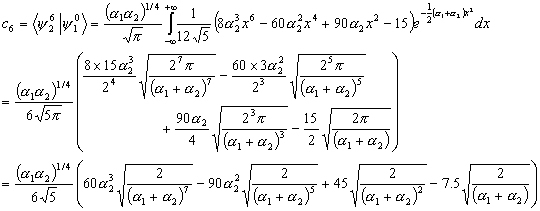
The equation for the wavefunction at t = 0 becomes

Since the eigenvalues for state 2 are given as
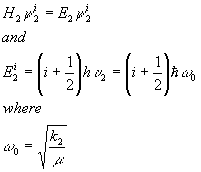
The time dependence can be written in to the equation by
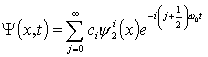
Substituting the appropriate wavefunctions and eigenvalues I obtain the time dependant solution.

This is our final result for the time dependant wave equation propagating in time.
The probability as a function of position and time can be
written as