Chapter 4:              The Degradation of Sarin

 

 

 

 

4.1        Motivation

 

Sarin, also known by its US designation as GB, is one of a number of toxic organo-phosphoric compounds.  The chemical name for GB is isopropyl methylphosphonofluoridic acid (C₄H₁₀FO₂P).  A German scientist by the name of Dr. Gerhard Shrader first synthesized GB in 1938 while studying the possibility of using organo-phophorous substances as pesticides.  The name Sarin was derived from the names of the researchers on the project (Schrader, Ambros, Ritter, and Linde).  Dr. Shrader soon realized that a small amount of GB can be lethal in minutes by either inhalation or physical contact and, therefore, had military applications as a chemical weapon.  GB kills by disrupting the nerve impulses, causing the victim to die by suffocation.  For this reason it is referred to as a nerve agent.   GB is an odorless liquid with a relatively high volatility, when compared to other nerve agents.   Although more toxic nerve agents have been synthesized, like the VX class of nerve agents, GB is still the chemical weapon of choice, since it is relatively inexpensive and easy to synthesize. 

Once released in to the environment, GB will begin to undergo hydrolysis, reacting with water or the Hydroxyl radical (OH), resulting in the production of isopropyl methylphosphonic acid (IMPA) and HF.  IMPA will react with a second water molecule producing other substances like isopropynol and methylphosphonic acid.  The focus of this work will be on the degradation of GB with the production of IMPA and HF and on the degradation of GB by reaction with the OH radical.

There have been many studies done with regard to the neutralization of nerve agents by acidic, neutral, and basic solutions [47-50].  Although GB will react with the H₂O molecule and the OH radical under these conditions, it is observed that the rate of neutralization is dependent on the pH level of the solution.  Basic compounds having a high pH level, like NaOH, will result in a higher rate of neutralization than neutral or acidic solutions.  The half-life of a solution of GB and water is approximately 100 hours.  If a salt is added to the water to increase the pH level (becoming more basic) the rate of degradation of GB will increase.  A solution of sodium hydroxide (NaOH) is commonly used in the neutralization or destruction of GB and other nerve agents.

There are several areas of research with regard to GB and its precursors.  One area of study is the identification and remote sensing of GB, its precursors, and reaction products by the detection of passive Long Wave Infrared Radiation (LWIR) [51,52].   Jenkins et. al. [53] has investigated new ways of using polymer based luminescent sensors to detect the presence of Sarin and Soman through hydrolysis.  In 1986 Politzer et. al. [54] studied the possibility of making Sarin less toxic by replacing the fluorine atom by another functional group.  In that work ab-initio SCF molecular orbital calculations using small basis sets were performed on several chemical groups, including the hydroxyl radical, OH.   This work resulted in a first step at analyzing the reactions of GB and radicals.   Other work includes the study by Samuels et al [55] on the potentials of using microwave spectroscopy in the detection of nerve agents.   In 1988 a group from Aberdeen Proving Ground used Hartree-Fock methods and MP methods to evaluate the potential military uses in calculating the molecular structures, harmonic vibrational frequencies, and IR intensities for a number of chemical agents [56,57].  The remote sensing of chemical agents released in to the environment can be detected by using LWIR hyperspectral sensors.  The identification and classification of the chemical agents depend on an accurate determination of the vibrational spectra of the chemical agents.   Ab-initio calculations to determine the harmonic vibrational spectra of a molecule could be used in this identification process.  However, there are only a few calculations.  One ab-initio calculation of the rotational spectra was performed by Walker et al. [58] for two GB isomers.

The use of ab-initio methods to determine the physical properties, molecular structures, chemical reactions, energy, vibrational frequencies, etc. removes the potential hazards of handling the substance in laboratory environments. The study also leads to a better understanding of how GB reacts with various constituents in the atmosphere.   In this chapter we investigate the energy surface landscape, minimum energy structures, transition structures, and possible reaction path of GB reacting with water and the OH radical.  The study should lead to a better understanding of how GB reacts with constituents in the atmosphere.  A summary of the chemical data for GB is given in Table 4.1.

 

Table 4.1:  Chemical data for GB

 

Molecular Formula	C4H10FO2P
Chemical Name	Isopropyl Methylphosphonofluoridic acid
U.S. Designation	GB
Formula	CH3 _ P (= O)(_F)(_ OCH(CH3)2)
Molecular Weight	140.09 amu
Density	1.089 g/cm3
Melting Point	-57o C
Boiling Point	147o C
Vapor Pressure at 20o C	1.48 torr (mm of Hg)

 

The optimized structures of several nerve agents using B3PW91/6-311g(d) are shown in Fig. 4.1.  All the structures of the nerve agents include two oxygen atoms, one that has a single bond with the phosphorus atom and the other is doubly bonded to the phosphorus atom.  In addition, GB, GD, and GF have a fluorine atom that is bonded to the phosphorus atom.  The nerve agents GA, GB, GD, and GF have stereo isomers that can be found by interchanging the fluorine and doubly bonded oxygen atom in GB, GD, and GF, and in GA by interchanging the C-N with the doubly bonded oxygen atom.  The nerve agent, VX, has four related isomers that are found by interchanging the ordering of the oxygen and sulfur groups about the phosphorus atom.  The isomer of GB studied here is GB-R, which differs from GB-S by an exchange of the Fluorine atom and the doubly bonded oxygen atom.  

 

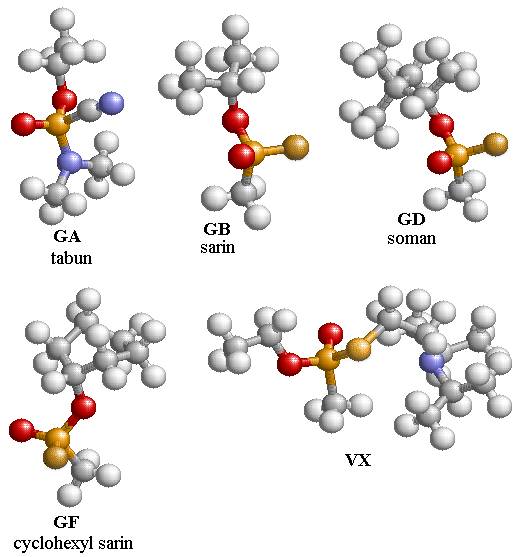
Figure 4.1:  The optimized structures of several nerve agents using B3PW91/6-311g(d).  The colors are Oxygen (red), Phosphorous (light yellow), Fluorine (gold), and Nitrogen (blue).  Note that the gold atom on the VX nerve agent is Sulfur.

            The chemical properties of the nerve agent are given in Table 4.2.  The density, vapor pressure, and volatility values are given for temperatures of 25^o C.  GB is the most volatile of the nerve agents having a value of 17,000 mg/m³, and has a vapor pressure of 2.9 mm of Hg.   All the nerve agents have nearly the density of water.  

 

Table 4.2:  Chemical data for the nerve agents in Fig. 4.1.

 

Properties	GA Tabun	GB Sarin	GD Soman	GF Cyclohexyl sarin	VX
Molecular weight	162.1	140.1	182.2	180.2	267.4
Density (g/cm3)	1.073	1.089	1.022	1.120	1.008
Boiling-point (oC)	247	147	167	~92	300
Melting-point (oC)	-50	-56	-42	< -30	-39
Vapor pres. (mm Hg)	0.07	2.9	0.3	0.06	0.0007
Volatility (mg/m3)	600	17,000	3,900	600	10

 

 

Table 4.3:  Bond lengths for the nerve agents in Fig. 4.1.  Values are in Å.

 

Properties	GA, Tabun X=CN	GB, Sarin X = F	GD, Soman X = F	GF, Cyclohexyl sarin, X = F	VX X = S
P-X	1.81	1.60	1.60	1.60	2.11
P-O	1.47	1.47	1.47	1.47	1.49
P-OC	1.59	1.59	1.59	1.59	1.62

4.2                       Hydrolysis of GB: A Density Functional Study

 

In the first part of the research, I found the transition structure and energy barrier in the reaction between GB-R and H₂O.  A geometric optimization was performed using density functional hybrid, B3PW91/6-311g(d), for each of the reactants and products in the chemical reaction shown schematically in Fig. 4.2.  This was followed by a frequency calculation to verify that each structure was a stable structure.   A search was systematically made for the transition structure.  As the water molecule approaches the fluorine atom, as in Fig. 4.3(a), the fluorine atom becomes displaced from its original position until a transition structure is formed, as shown in Fig. 4.3(b).  Simultaneously, the fluorine atom forms a bond with one of the hydrogen atoms in the water molecule, forming HF, which is finally expelled from the system leaving as a product the molecule of IMPA, as shown in Fig. 4.3(c).  The height of the energy barrier for this reaction was found to be 38.6 kcal/mol.  This figure provides the energy balance of the reaction as well as the IRC path along the potential energy surface followed during the reaction.

The geometry changes are schematically given in Table 4.4.  This table contains also the charge on each atom as calculated from a Mulliken analysis of the wave function.

 

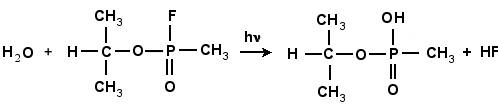
Figure 4.2:  The reaction of GB with H₂O forming HF and IMPA.

 

 

Table 4.4:  Listing of the relative energy values and the relevant distances and angle for the reaction shown in Fig. 4.3.

 

 

 

 

According to transition state theory the relationship between the reaction rate constant, k_R, activation energy or energy barrier, E_a, and temperature, T, is given by

 

 

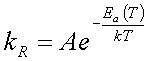                                                                      (4.1)

 

 

which is known as the Arrhenius equation.  For large energy barriers and keeping the temperature constant, the reaction rate decreases resulting in a less probable reaction.

The constant can be calculated more precisely using the approach of D. H. Lu et al. [59].  In this thesis I have not pursued a very exact calculation of k_R.   In what follows I only give estimates of the energy barrier without inclusion of the thermal contribution coming from the vibrations.  However, if one wants to calculate this thermal energy in the harmonic approximation, then Eqs. 3.12 and 3.15 should be used.  In this particular calculation, the thermal correction to be added to the energy of the minima are also given in Table 4.4 for T = 300 Kelvin.

 

The same calculation for the reaction in Fig. 4.1 was carried out at the HF level, with the D95** basis set.  In this case the geometry of the reactant and products (Table 4.4 and Fig. 4.3) is not significantly different than that obtained with B3PW91.  However, the energy barrier is now 60 kcal/mol (see Fig. 4.4).  The discrepancy in the barrier calculation is to be expected since density functional is not a well-suited approximation to calculate barriers where a significant amount of charge transfer is involved. We believe then that the HF value is a more realistic number to represent this reaction.  Fig. 4.4 shows the one-step IRC reaction path calculated within the HF/D95** approximation and B3PW91/6-311g(d) method for GB reacting with H₂O.  Information in these graphs is very important for an exact calculation of the rate constant.  For example, the code known as “polyrate”, developed by D. Truhlar et al. [60] requires not only the values of the barrier, but also the values of the energy surface along the reaction path as given in the IRC plot.

 

 

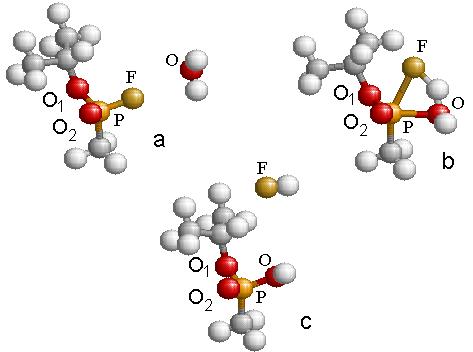
Figure 4.3:  The reaction path representing the hydrolysis of GB resulting in the formation of IMPA and HF within the B3PW91/6-311g(d) approximation.

 

 

 

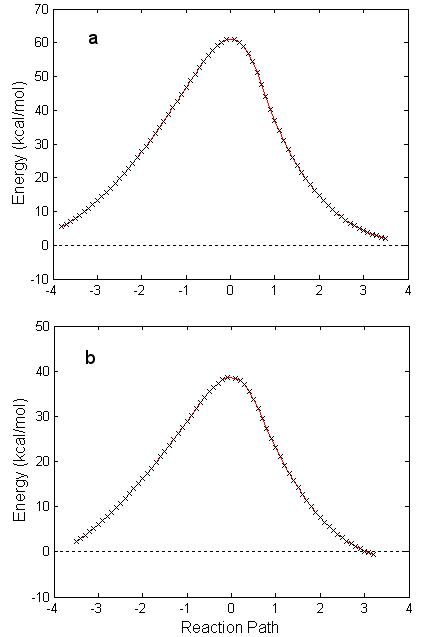
Figure 4.4:  An IRC one-step reaction path of GB reacting with water using (a) HF methods and (b) B3PW91/6-311g(d) resulting in the formation of IMPA and Hydrogen Fluoride.

 

 

 

4.2        The Vibrational Modes of GB and IMPA

 

A frequency calculation was done using GGA for GB and IMPA.  A listing of the frequencies having IR intensity higher then 40 is given in Table 4.5 for GB and in Table 4.6 for IMPA.   The identification of nerve agents, or its precursors, depends on the ability to be able to distinguish between two similar spectra.  In the spectrum of GB, Fig. 4.5, the black lines indicate regions of the spectrum that are absorbed by the atmosphere, while the red lines represent spectral lines that are detected in the atmosphere.  Since GB has a much higher vapor pressure than other nerve agents it will evaporate more readily, and can be detected from a distance easily by using LWIR spectrometers.  In the field of remote sensing of chemical agents it is often necessary to make a chemical identification based on a limited number of lines that are not absorbed by the atmosphere in the LWIR.  The chemical bi-product of GB in its reaction with H₂O is IMPA, which has a spectrum that is similar to GB is shown in Fig. 4.6.  For this reason we conclude that it would be difficult to detect with LWIR a correct concentration of GB or its products of reaction in air.  However, this technique could be very useful to supplement the ultra sensitive, ultra rapid, mass spectrometer in-situ measurements.

The three strongest modes of vibrations shown in Figs. 4.5 and 4.6 are the stretching of the P-O bonds and the P-F bond in GB and the stretching of the three P-O bonds in IMPA.  The actual displacement for the three modes of vibration are depicted in Fig. 4.7 and 4.8 where the animation sequence goes from left to right.  The strongest line occurs at a frequency of 1019.9 cm^-1 and is the stretching mode of the P-O (isopropyl group) bonds, where the oxygen atom oscillates between the phosphorus and carbon atom.   This motion involves the alternating stretching of the P-O bond and the O-C bond.  A rocking motion of the isopropyl and methyl groups accompanies the stretching motion.  In the second strongest line at 1312.6 cm^-1 there is a stretching of the P=O bond.  The reason for the higher frequency is due to the double bonding (higher spring force) of the oxygen atom to the phosphorus atom.  This vibrational mode also involves the rocking motion of the isopropyl and methyl group while the other oxygen atom and fluorine atom remains nearly stationary.  The third strongest mode of vibration at 824.1 cm^-1 involves the stretching of the P-F bond, with rocking of the methyl group in GB.  A calculated spectrum of GB from 400 cm^-1 to 1500 cm^-1 is shown in Fig. 4.5.   The vibrational modes for IMPA are very similar to the modes of GB, as shown in Fig. 4.6.  The frequencies are close and there is a one to one correspondence in the modes of vibration

 

Table 4.5:  Frequencies and IR intensities for the strongest vibrational modes (intensities>40) of GB.

 

 

Table 4.6:  Frequencies and IR intensities for the strongest modes (intensities>40) of IMPA.

 

 

 

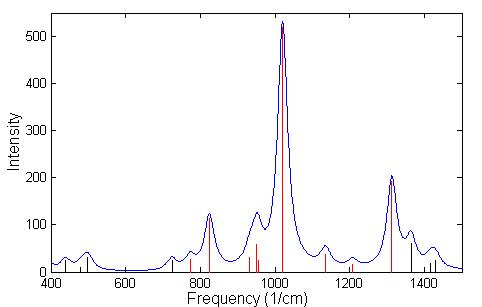
Figure 4.5:  Spectrum of the vibrational modes of GB.  The broadening of the lines was performed using a lorentzian distribution with a linewidth at Full Wave Half Maximum (FWHM) of 18 cm ^–1.  The red lines indicate the spectral lines that fall within the atmospheric window.

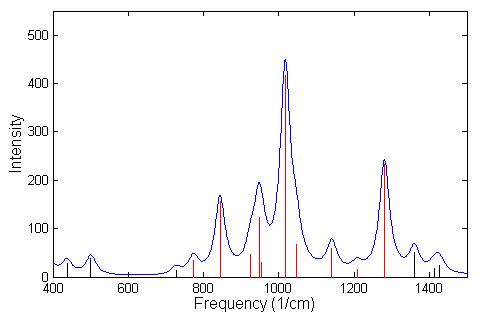
Figure 4.6:  Spectrum of the vibrational modes of IMPA.  The broadening of the lines was done using a lorentzian distribution with a linewidth at FWHM of 18 cm ^–1.  The red lines indicate the spectral lines that fall within the atmospheric window.

 

 

 

Figure 4.7:  The three strongest vibrational normal modes of GB are depicted by a series of instantaneous subsequent molecular conformations.

Figure 4.8:  The three strongest vibrational normal modes of IMPA are depicted by a series of instantaneous subsequent structures.

 

4.4           Reaction of GB with OH: A Hartree-Fock Study

 

In this part of the investigation, I performed an all-electron calculation at the Hartree-Fock level using the Dunning/Huzinaga [4] double zeta basis set with the addition of a ‘p’ polarization function for the hydrogen atom, and ‘d’ polarization functions for all the other atoms (abbreviated HF/D95**).   The inclusion of the polarization functions was important to ensure a precise geometric optimization of GB and a lower energy value.  Since the systems we will be working with in this part of the investigation are radicals (contain an odd number of electrons), or open-shell systems, it was better suited to use the HF method in the investigation, since DFT may not adequately describe behavior where charge transfer is important.  The criterion for convergence of the electronic energy in the self-consistent field (SCF) was approximation 10^-6 atomic units.  While calculating the reactant structures and the transition state structures, frequency calculations of the normal modes of vibration were performed to determine if the geometry is a minimum of the energy surface (frequencies are real) or corresponds to a saddle of the energy surface identified as a transition structure (one imaginary frequency).   The optimized geometry of GB did not deviate too much from the structure obtained earlier using B3PW91/6-311g(d).  

The geometries of the reactants, GB and OH, were optimized first.  One possible reaction involving the degradation of GB is the abstraction of the fluorine atom.  The OH hydroxyl approached GB along a line that was extended outward from the P-F bond and heading toward the fluorine atom, as in Fig. 4.9.  However, during this study I have determined that the fluorine abstraction reaction by OH can occur only if an intermediate radical (GB+OH)* is formed.  This new compound is very stable but can undergo a unimolecular reaction and liberate F and IMPA.  This degradation channel is not unique and therefore reaction-rate theory is not adequate for the description of this reaction.   Similarly, the established method of IRC to follow the reaction path on the potential energy surface is not valid.

Alternatively, I used the Nudged Elastic Band (NEB) method, [13-16] in conjunction with ab-initio “force” calculations to determine the energy barriers.  The NEB Method, as described in Chapter 2, the method allowed me to locate the transition structures based on force and single point energy calculations and is a good alternative to other methods that rely on gradient calculations.  The following steps were used in employing the ab-initio-NEB method to identify the barrier in each reaction: i) a linear interpolation between the coordinates of the products and reactants was performed to obtain ten “images” used in the NEB method; ii) all-electron single point energy and force calculations were performed on each image; iii) both the geometries from (i) and the force values from (ii) were used as input to the NEB method; iv) the atoms of each image were moved along the lines of force using  a variant of the Velocity-Verlet method;  the previous steps (ii-iv) were repeated until the energy between successive iterations converged to five decimal digits.

 

 

 

Figure 4.9:  Configuration of GB-R and OH before reaction.

 

4.5           The Various Reaction Elements of GB with OH

 

GB and other phosphorous-type compounds are prone to undergo hydrolysis, or neutralization, under basic conditions (temperature, OH-, hydroxyl ions).    In the neutralization of GB with the neutral hydroxyl radical (OH*), the bond between the phosphorous and fluorine atom breaks and F is liberated.  This process can occur either a one or two-step process.  The reaction scheme is shown in Fig. 4.10 and 4.11.  In the one-step process, the fluorine atom is combined with the hydrogen atom of the incoming OH, as shown in Fig. 4.10.  In the two-step process the hydroxyl radical, is inserted into GB, forming a very stable intermediate compound, GB+OH.  This compound subsequently degrades by unimolecular reaction either ejecting the F atom, or by liberating HF as shown in Fig. 4.11. This intermediate compound is a complex structure that includes both the GB molecule and (OH)*.  

The purpose of the investigation will be to study the reaction paths that lead to a degradation of GB and to determine the structure of the intermediate compound, the energy barrier needed to form it, and to find the structure of the activated compound (or transition state) for the reactions shown in Fig. 4.10 and 4.11.  In kinetics theory the transition state is an energy barrier in the reaction pathway.

Fig. 4.12 shows the sequence of structures and a plot of the energy balance with the one-step reaction path leading to the breaking of the P-F bond and the liberation of HF from the molecular system.  Table 4.7 lists relevant bond distances and charges during the three steps depicted in Fig. 4.12.  The energy required for this reaction is high, 66.1 kcal/mol.  Therefore, for this reaction to take place a catalyst needs to be added to the system.  The IRC path of the reaction is shown in the lower portion of Fig. 4.12.  The energy barrier is of the same order as that of the reaction GB + H₂O.  We believe that the reaction calculated at the HF level is more realistic than the reaction calculated within the DFT method.  The reason is that during the reactions of GB with H₂O or OH there is a very important charge transfer needed to break the P-F and O-H bonds and form the H-F bonds.

 

 

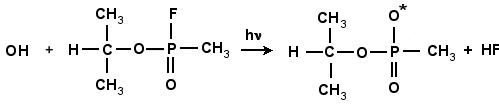
Figure 4.10:  The reaction of GB with OH.  The resulting products are the isopropyl methylphosponate radical and HF.

 

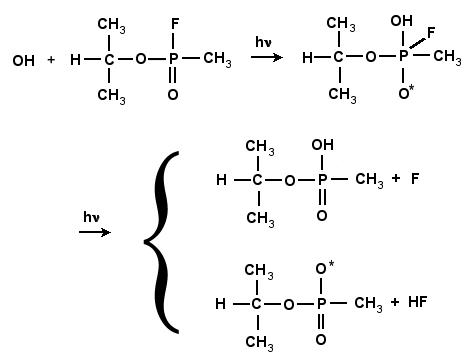
Figure 4.11:  Reactions of GB with OH leading to the formation of an intermediate compound, followed by two possible unimolecular reactions leading to either the formation of IMPA and the abstraction of the F atom, or a radical and the formation of HF.

 

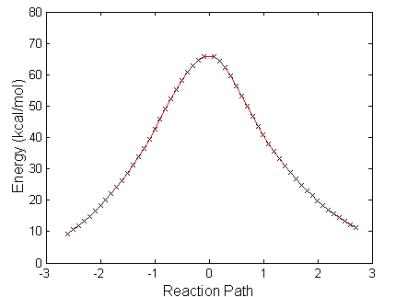
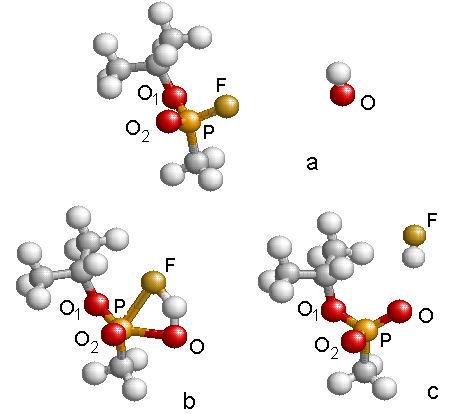
Figure 4.12:  Geometric structures resulting in the reaction of Fig.4.10.  Energies are referred to GB +OH at infinity.  Step ‘a’ is the reactants with infinite separation, step ‘b’ is the transition state, and step ‘c’ is the products separated by a large distance.  The IRC plot of the reaction is provided.

Table 4.7:  Listing of the relative energy values and the relevant distances, angles and charges for the reaction shown in figure 4.12.

 

 

 

 

 

In the study of the two-step reaction of Fig. 4.11, the best geometry of the GB-OH intermediate compound was obtained with the same precision as that of GB and OH.  This intermediate compound is very stable, only 3.9 kcal /mole above the energy of GB plus OH at infinity.  In this intermediate compound, CH₃PO[OCH(CH₃) ₂]FOH, the phosphorous atom is pentavalent with one unsaturated oxygen atom.  The geometry details are reported in Table 4.8 (step 3).  Steps along the reaction path GB+OHàGB-OH* were determined using the ab-initio and NEB method.  The NEB method allowed the determination of the transition structure that corresponds to a reaction barrier of 76.8 kcal/mole.  The geometry of the transition structure is given in Table 4.8 (step 2).  A schematic representation of this reaction is given in Fig. 4.13 where step 1 depicts the two molecules before reaction, step 2 corresponds to the transition structure and step 3 shows the geometry of the intermediate radical GB+OH*.

            Subsequently, the newly formed intermediate radical decays following two different unimolecular breakdown paths. In one, Fig. 4.14 steps 4 and 5, the fluorine atom is ejected and IMPA is formed.  A barrier of 25.6 kcal/mole was found using the NEB method. The transition complex for this reaction presents a stretched F-P bond while the isopropyl and hydroxyl groups rotate slightly one toward the other. The geometry of this transition structure is reported in Table 4.9 (step 4) and a schematic energy representation is given in Fig. 4.14.  Step 5 shows the final geometry of the IMPA molecule once the F atom has been liberated.  The geometry of this molecule is reported in Table 4.9 (step 5).  This is the only possibility to abstract the Fluorine atom.

In the other unimolecular reaction, bottom of Fig. 4.11, hydrofluoric acid is produced with the formation of a radical.  A charge transfer favors the formation of the new F-H bond while the P-F bond weakens and finally breaks. The HF molecule leaves the system and the oxygen atom that belonged to the OH replaces the Fluorine atom, as shown in Fig. 4.15.  The reaction needs to overcome a barrier of 20.8 kcal/mole, slightly less energy than the previously described reaction.  This reaction, in going from Fig. 15 (step 3) to Fig. 15 (step7), is exothermic liberating 7.2 kcal/mole of thermal energy.  The geometry of the HF and remaining radicals are given in Table 4.9 (step 6 for the transition structure and step 7 for the final compounds).   As in the previous unimolecular reaction, the reaction barrier was determined with the NEB method.

 

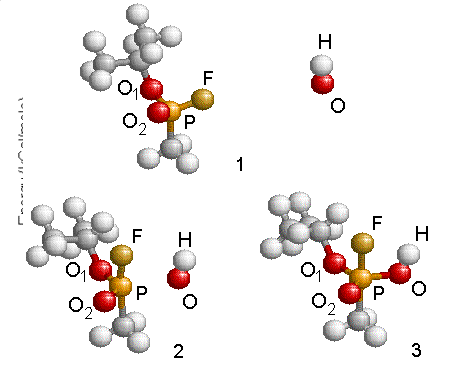
Figure 4.13:  Reaction schematic shows the approach of the OH radical to GB and the formation of the intermediate structure.  Energies were referenced to that of the GB and OH at infinity.

 

 

 

 

 

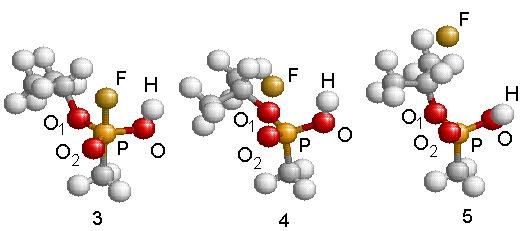
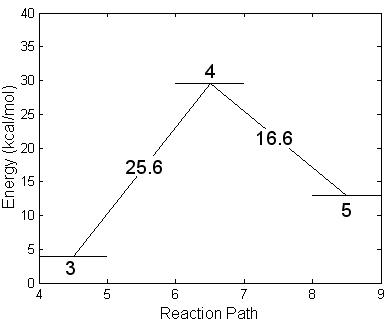
Figure 4.14:  Geometric structures resulting in the formation of IMPA after expelling the fluorine atom when the intermediate radical GB+OH* decays.  The energy balance shown at the bottom reports energies referenced to GB and OH at infinity.

 

 

 

 

 

 

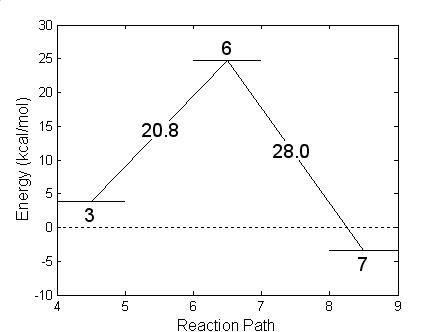
Figure 4.15:  Geometric structures resulting in the formation of isopropyl methylphosphonate radical after expelling hydrofluoric acid (Fig. 4.13.).  The energy balance shown at the bottom reports energies referred to GB + OH at infinity. 

 

Table 4.8. Geometry and the calculated charges of reactants and products in the chemical reaction of GB with OH depicted in Fig. 4.13.  Charges are in units of the elemental charge e.

 

	GB and OH at Infinity Step 1	Transition Structure Step 2	GB-OH* Step 3
E (kcal/mole)	0.0	76.8	3.9
P-C (Å)	1.79	1.83	1.84
P-O1 (Å)	1.58	1.59	1.59
P-O2 (Å)	1.46	1.60	1.63
P-F (Å)	1.58	1.58	1.69
P-O (Å)	infinity	2.37	1.61
O-H (Å)	0.96	0.96	0.95
O2-P-O1 (o)	117	121	121
O2-P-F (o)	111	84	83
O1-P-F (o)	102	93	92
F-P-C (o)	102	173	173
O1-P-C (o)	104	95	93
O2-P-C (o)	118	93	90
F-P-O (o)	0	84	88
O1-P-O (o)	102	117	118
O2-P-O (o)	111	121	121
P-O-H (o)	90	111	113
Charge on P	1.41	1.25	1.47
Charge on F	-0.44	-0.43	-0.54
Charge on O1	-0.61	-0.59	-0.61
Charge on O2	-0.71	-0.31	-0.32
Charge on C	-0.52	-0.49	-0.53
Charge on O	-0.34	-0.59	-0.63
Charge on H	0.34	0.34	0.37

 

 

Table 4.9.  Geometry and charges of transition state and products compounds in the two unimolecular reactions of the intermediate radical GB-OH^* depicted in Fig. 4.14 and 4.15.  Charges are in units of the elemental charge e.

 

 

 

4.6        Conclusion

 

In the endothermic reaction of GB and H₂O, the energy needed to overcome the energy barrier is 60.6 kcal/mole.  In this reaction the chemical products HF and IMPA are produced, having a net relative energy of 6.69 kcal/mole.  At the GGA level the energy barrier is 38.6 kcal/mole.

The single-step reaction of GB with OH requires energy of 66.1 kcal/mole to take place at the Hartee-Fock level of approximation.  The two-step reactions of GB with OH are improbable reactions under normal conditions because an initial barrier of 76.8 kcal/mole is needed to start the reaction.  It is observed that if 76.8 kcal/mole are available, the formation of the (GB+OH)* neutral radical is possible.  If the neutral radical is formed then two possible unimolecular reactions can proceed as shown in Fig. 4.14 and 4.15.  The energy barrier that is needed for the abstraction reaction of fluorine is 25.6 kcal/mole, whereas only 20.8 kcal/mole are required to liberate HF.  The later is exothermic with the release of 7.2 kcal/mole.