Chapter 2:
Theory
2.1
Born-Oppenheimer
Approximation
The Schroedinger equation is the basic equation governing the
interactions between atoms and molecules, and yet it can only be solved
analytically for the hydrogen atom. For
other elements, systems of atoms, or molecules, we must use approximations to
the Schroedinger equation. The three
important approximations made in the study of molecular systems are the
Born-Oppenheimer approximation, Hartree-Fock (HF) approximation, and the
assumption that the total wavefunction can be expressed as a Linear Combination
of Atomic Orbitals (LCAO). The
Born-Oppenheimer approximation comes about from the large difference that
exists between the mass of an electron and the mass of the nucleus. The nucleus can be considered as stationary
in space while the electrons moves around the nuclei. In the Hartree-Fock approximation the motion of electrons are
influenced by the average field that is generated by contributions from all the
other electrons in the atomic or molecular system. Any correlation between the motions of electrons is neglected in
this approximation. The third
approximation relates to expressing the total wavefunction as a LCAO. The true representation of the molecular
orbital is approximated by the LCAO, which consists of an expansion in a set of
basis functions. The type of basis
function used and the finite size of the basis set (section 2.3) used in the
LCAO, are limiting factors in the approximation to the true representation of
the molecular orbital.
The first approximation used in the study of atomic and molecular system is to simplify the Schroedinger equation by treating the motion of the electrons and nuclei
separately. For a system of many atoms and electrons one can solve for the electronic
part and the nuclei
part separately. The total wavefunction
can be written as the product of the electronic and nuclear parts of the
wavefunction, with the electronic portion depending parametically on the
position of the nuclei. This is the essence of the Born-Oppenheimer
approximation. The general expression
for the wavefunction can be written as
(2.1)
Where ‘r’ is the
position vector of the electrons, ‘R’ is the position vector of the nuclei, and
the subscripts ‘e’ and ‘n’ refers to the electrons and the nuclei,
respectively. The electronic
wavefunction is a function of the position of the electrons and depends
parametrically on the nuclei positions while the nuclei wavefunction is a function
of only the position of the nuclei.
In the study of atomic and molecular systems the distribution and
behavior of the electrons will define the structure and properties of
matter. If we desire the total
energies, we can simply add to the Hamiltonian (H) the energy of the nucleus to
the energy of the electrons. The
Schroedinger equation can then be written in two parts, the electronic and the
nuclear part.
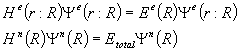(2.2)
The electronic part
of the Hamiltonian is a function of the position vector of both the electrons
and nuclei, while the nuclear part of the Hamiltonian is dependant only on the
nuclear position vector.
The electronic Hamiltonian, which does not contain the kinetic energy of
the nuclei, can be written as a summation of the electronic kinetic energy,
electron-nuclei coulomb interaction,
electron-electron coulomb interactions, and nucleus-nucleus coulomb
interactions.
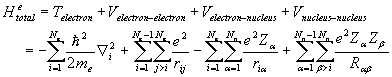(2.3)
Where ‘Ne’
is the number of electrons, ‘Nn’ is the number of nuclei, ‘Z’ is the
ionic charge, ‘e’ is the charge of an electron, me is the mass of an
electron ‘T’ is the kinetic energy, and ‘V’ is the potential energy. The second, third and forth term of the
above equation are the total potential energies arising from coulomb interaction between electron-electron,
electron-nuclei, and nuclei-nuclei pairs
The Hamiltonian for the nuclei is the sum of the kinetic energy of the
individual nuclei and the electronic energy, which was found from the solution
of the Schroedinger of the electronic Hamiltonian and can be written as
(2.4)
2.2
Hartree-Fock
Approximation
The total energy of the atomic or molecular system contains the
electronic kinetic energy and the potential energies. The total energy for a closed electronic configuration (even
number of electrons) can be written as
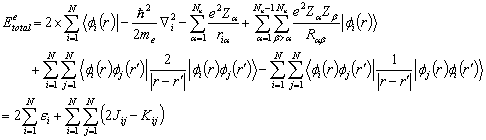(2.5)
where fi(r) are the atomic orbitals of the basis set in the LCAO, Ne
and Nn are the number of electron and nuclei, respectively. The molecule is described by ‘N’ occupied
orbitals (each orbital contains 2 electrons) in a closed shell configuration, J
is the coulomb integral, or the electrostatic repulsion between 2 charge
distributions, and K is the exchange integral from the Pauli principle and
fermion nature of the electrons. The
one electron energy of the electrons is characterized by ei.
The main difficulty with the HF method is the lack of electron
correlation. The HF method will
determine an upper bound for the true energy of the atomic or molecular
system. As the size of the basis set
used in the calculation becomes larger, the upper-bound energy value will
decrease until a point is reached where no further increase in basis set size
will result in a decrease in energy.
The value of the energy at this limit is known as the Hartree-Fock
energy. The true energy of the system
will always be lower then the expectation energy calculated using a given trial
function. The variational method
minimizes the expected energy with respect to the coefficients in the LCAO
expansion such that
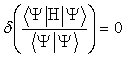(2.6)
The computational
time will increase with the size of the basis set. Therefore, a balance will need to be reached between the size of
the basis set and computational effort.
The difference between the HF energy and the true energy is referred to
as the electron correlation and is defined by
(2.7)
The electrons in a
system of atoms or molecules will tend to avoid one another more than is
predicted by the HF equation.
Moller-Plesset Perturbation Theory (MP2 and MP4) theory is an attempt to
include some of the correlation terms in to the HF method. The MP method involves treating the
correlation as a perturbation to the Hamiltonian, as seen in the equation
below.
(2.8)
Where ‘l‘ is a parameter that determines the strength of
the perturbation. Another way to include correlation is by using density
functional methods [1,2] or density functional hybrids (section 2.5 and
2.6). In my treatment of the calcium
clusters and calcium carbonate clusters I will be using the density functional
hybrid method to include the correlation effects.
2.3
Basis Sets
The interpretation of the wavefunction, y, stems from quantum mechanics and the probabilistic and quantized nature of quantum
mechanics. If we know the wavefunction
of the system of particles, in principle, we can determine all observable
quantities of the chemical system being investigated. The interpretation of
y
can be seen from |y|2, where |y|2
represents the probability of finding an electron
in a particular region of space. The
probability is often associated with electron density or probability density
when calculated per unit volume. In a
molecular system we can define the wavefunction as a linear combination of
gaussian type functions.
(2.9)
where ‘c‘ is the
molecular orbital coefficients, ‘f‘ is a function, and the summation is over the complete basis set of
functions. The molecular orbital
coefficients are the quantities that are varied in such a way as to give the
minimum expected energy (Eq. 2.6).
Gaussian functions are used in the basis function since they are easier
to manipulate in integrals, resulting in less computational effort. A basis function can be defined by
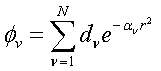(2.10)
Where the
coefficients, d and a, are sets
characterizing different elements:
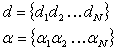(2.11)
The summation is over
a limited number of gaussians making up the basis set. The basis set is centered on each atomic
nucleus in the molecule and resembles the mathematical quantities defining the
electronic orbitals. Every basis set
has a set of coefficients, ‘d’, and exponents, ‘a’. Both quantities stay fixed throughout the Hartree-Fock calculation. The criterion used in choosing a basis set
is the ability to accurately predict chemical results at reasonable
computational costs. As the size of the
basis set increases so does the computational effort and time. The energy decreases with increasing basis
set size, approaching the Hartree-Fock limit where any further increase in the
size of the basis set leads to a negligible decrease in the energy.
The minimum basis set is the STO-3g basis set. As the size of the basis set increases, the Hartree-Fock limit is
reached. With a basis set having an
infinite size we would be at the Hartree-Fock limit.
(2.12)
A triple split valence basis set, 6-311g, has six primitive gaussians
for the core orbital and three basis functions for the valence orbital
represented by three, one, and one primitive gaussian. The three basis functions for the valence
orbitals have different
exponents. For the calcium atom in the
study of calcium clusters and calcium carbonate clusters, I used eight ‘s’,
seven ‘p’, and one ‘d’ gaussians contracted or (62111111,3311111,3) primitive
gaussians contracted as (8s,7p,1d) and augmented with one ‘d’ polarization function (see Table 2.1). The basis set is
abbreviated 6-311g(d). Split
valence basis sets allow for polarization orbitals with different
exponents. I
found this basis set to be sufficiently large to give good results at a
reasonable computational effort. A listing of the coefficients, d and a, are
shown in Table 2.1 [3]. Adding
an additional diffuse or polarization function produced insignificant changes
in both the energy and bond lengths in our study
of calcium clusters and the study of calcium carbonate clusters.
To arrive at the total
binding energy (Eb) of a system of calcium atoms, the total energy
obtained from the quantum mechanical results, E(cluster), is subtracted from
the product of the energy of a single calcium atom, E(atom), and the number of
atoms.
(2.13)
where N is the number of atoms in the
cluster. For the large basis sets that
we used in the study of calcium clusters, this equation is a close
approximation to the actual binding energy.
There is no need to include a correction term. However, for smaller basis sets the error becomes more
significant. A more accurate
representation of the binding energy can be written as
(2.14)
Where BSSEC refers to a Basis Set Superpostion
Error Correction (BSSEC). Since the
basis set is centered on each atom in the cluster, the total energy of the
system can be influenced by the overlap of the basis set from one atom with the
basis set of a neighboring atom, that is the basis set centered on one atom
will “interfere” with the basis set on all other atoms in the cluster. This has the net effect of lowering the
energy in the first term resulting in a higher value for the binding
energy. The second energy term assumes
an isolated atom and basis set. In
order to compensate for the energy a BSSEC is added to the equation. Programmatically, what is done is to
generate a basis set centered on the positions of all the atoms in the cluster
and than remove all but one atom, followed by a single point energy
calculation. Repeat this for each atom
in the cluster and then add the energies.
This will give us the second term in equation 2.1. By doing this we maintain the continuity of
the basis set between the first and second term of equation 2.1.
The analysis involving the degradation of sarin with OH used the Dunning/Huzinaga basis set [4] augmented with a ‘d’ polarization function for heavy atoms and a ‘p’ polarization function on the hydrogen atom (D95**). This basis set is a full double zeta, double zeta for the core and valence orbitals. That is, it has twice the number of basis functions than a minimal basis set (STO-3G). There are has 2 ‘s’ type basis function (1s and 1s’) for the hydrogen atom, for first row atoms there are 4 ‘s’ type basis functions (1s, 1s’, 2s, 2s’) and 2 ‘p’ type basis functions (2p and 2p’), or (6111,41) primitive gaussian type orbitals contracted as (4s, 2p). Note that the name, D95, was derived from the number of primitive gaussian used in the ‘s’ and ‘p’ orbitals of the first row atoms. All molecular orbitals are formed from linear combinations of two sizes of functions for each atomic orbital
.
Table 2.1: The basis set 6-311g(d) optimized to include the Ca atom. The basis set is (62111111,3311111,3) contracted as (8s, 7p, 1d), with an additional ‘d’ polarization function [3].
|
Exponents |
Contracted
Coefficients |
|||||||
|
|
1s |
2s |
3s |
4s |
5s |
6s |
7s |
8s |
|
0.2026990000D+06 0.3038250000D+05 0.6915080078D+04 0.1959020020D+04 0.6409359741D+03 0.2339770050D+03 |
0.2229639940D-03 0.1729320036D-02 0.9002259932D-02 0.3666989878D-01 0.1194100007D+00 0.2918249965D+00 |
|
|
|
|
|
|
|
|
0.9228919983D+02 0.3725450134D+02 |
|
0.4044150114D+00 0.2963129878D+00 |
|
|
|
|
|
|
|
0.9131979942D+01 |
|
|
1.0 |
|
|
|
|
|
|
0.3817790031D+01 |
|
|
|
1.0 |
|
|
|
|
|
0.1049350023D+01 |
|
|
|
|
1.0 |
|
|
|
|
0.4286600053D+00 |
|
|
|
|
|
1.0 |
|
|
|
0.6282260269D-01 |
|
|
|
|
|
|
1.0 |
|
|
0.2601619996D-01 |
|
|
|
|
|
|
|
1.0 |
|
Exponents |
Contracted
Coefficients |
||||||
|
|
2p |
3p |
4p |
5p |
6p |
7p |
8p |
|
0.1019760010D+04 0.2415959930D+03 0.7763700104D+02 |
0.2059859922D-02 0.1665009931D-01 0.7776460052D-01 |
|
|
|
|
|
|
|
0.2911540031D+02 0.1176259995D+02 0.4922890186D+01 |
|
0.2418060005D+00 0.4325779974D+00 0.3673250079D+00 |
|
|
|
|
|
|
0.1906450033D+01 |
|
|
1.0 |
|
|
|
|
|
0.7368999720D+00 |
|
|
|
1.0 |
|
|
|
|
0.2764199972D+00 |
|
|
|
|
1.0 |
|
|
|
0.6027000025D-01 |
|
|
|
|
|
1.0 |
|
|
0.1790999994D-01 |
|
|
|
|
|
|
1.0 |
|
Exponents |
Contracted
Coefficients |
|
|
|
3d |
4d |
|
0.1507999992D+02 0.3926000118D+01 0.1233000040D+01 |
0.3689470142D-01 0.1778199971D+00 0.4255129993D+00 |
|
|
0.2600000000D+00 |
|
1.0 |
2.4
Density
Functional Theory
In 1964 Hohenberg and Kohn [1] proposed that the ground state electronic energy of a system could be
written as a function of the electron density. This is the basis of the Density Functional Theory (DFT). The theorems that form the basis of the DFT
are
1.
(Uniqueness) The
ground state expectation value of any observable is a unique functional of the
exact ground state electronic charge density r(r).
2.
(Variational
principle) The electron charge density, r(r), minimizes the total energy of the system, E(r).
3.
(Universality) The
kinetic energy of a system of electrons can be expressed as a system of
non-interacting particles. This forms
the basis of the Kohn-Sham Scheme.
Kohn and Sham [2]
developed the self-consistent equations that carry their name where the exchange and correlation energy are
included through the functional of the density. In the DFT the total energy is
given by the sum of the potential energy terms and the kinetic energy
(2.15)
Where the charge
density, r, is a
function of the electron positions, T is
the kinetic energy, Ven is the electron-nucleus interaction, Vee
is the electron-electron interactions, and EXC is the
exchange-correlation energy. In the
Schroedinger equation the potential energy is a function of the electronic 3N
coordinates but in the density functional theory the potential energy is a
function of the charge density, which in turn is a function of spatial
coordinates. In effect by defining the
potential energy as function of spatial coordinates, we have simplified the
analysis of the N–particle problem by treating all electronic properties of the
system as a function of the charge density.
The result is an accurate approximation that does a good job at
predicting the energetics of materials.
In 1965 Kohn and Sham [2] developed a treatment of
the kinetic energy in a many body system of N-electrons by replacing the
wavefunction by a single-particle wavefunction, y(r). The kinetic energy in a system of
interacting particles having a given charge
density is equivalent to the kinetic energy in a system of non-interacting
particles having the same charge density.
The total electronic energy can be given by
(2.16)
Any
correction to the total energy is incorporated in to the expression for the
exchange-correlation energy, EXC.
The exchange-correlation functional is an approximation and is a
function of the local charge density, or the charge density and the gradient of
the charge density. The equation can be
solved self-consistently by starting with an initial guess for the charge
distribution, calculate the potential energy terms, and from the resulting
wavefunction, a new value for the charge distribution is found. Repeat the process until convergence is achieved
in the charge density.
2.5
Density
Functional Hybrids
The two types of approximations made in calculating the
exchange-correlation energy are the Local Density Approximation (LDA)
and the General Gradient
Approximation (GGA). In the LDA the electron
density is assumed to be constant over a localized region in space. In the GGA (a non-local correction to the
LDA) the charge density is slowly varying over a region in space. Exc is the exchange-correlation
energy of a uniform electron gas and in the GGA with spin polarization we have
the general expression
(2.17)
where ‘f’ is a
function of the electron density of the spin up and spin down electrons, and a
function of the gradient of the electron density for the spin up and spin down
electrons. In my study of the calcium
atoms all the electrons are in their ground state and any pair of electrons,
one with spin up and the other with spin down occupies one orbital.
In the study of calcium clusters and clusters of calcium carbonate, we
used a combination of the HF (exact) exchange and a gradient correctional term
in the Exc functional. This
is called the Becke’s three-parameter hybrid method [5-7]. The Exc may be local [8]. Perdew-Wang [9,10] (B3PW91) functional
provides the correlational terms, both
local and non-local. The local
correlation is just the LDA as described above. Beck’s 3-parameter hybrid method is defined by [7]:
(2.18)
where A, B, and C are
parameters. From the above equation we
see that the exchange-correlation energy is actually the sum of two functions,
an exchange part and a correlation part.
The contribution to the exchange energy includes the Slater exchange
energy (often referred to as the LDA for the exchange energy), Hartree-Fock
exchange energy (or the exact exchange), and a correction to the exchange
energy provided by Becke (DEXBecke). The correlation energy has a local (LDA)
part and a non-local part, or general gradient approximation (GGA), both are
given by the Perdew-Wang functional (PW91) [9,10].
The coefficients A, B, and C were determined by Becke [7] using a linear
least-square fit to experimental results in the G1 dataset provided by Pople
and coworkers [11]. The G1 dataset
contains 156 atomization energies, 42 ionization potentials, 8 proton
affinities, and the 10 first-row total atomic energies. From the least square fit, the values found
for the coefficients are A=0.80, B=0.72, and C=0.81. In the limit of non-interacting electrons, only the HF exchange
energy contributes to the exchange-correlation energy. In other words, the energy attributed to
the correlation terms is 0 and the exchange energy becomes the exact
exchange. The exact energy can be
calculated using HF methods.
ExHF is the exact Hartree- Fock exchange defined
by
with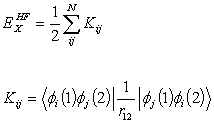 
(2.19)
Where Kij
is the exchange integral and the summation is over the molecular orbitals.
To satisfy the exact asymptotic behavior of a many-electron system,
Becke proposed a correction
to the LDA exchange energy, or gradient-corrected exchange functional, which is
defined by [5]
with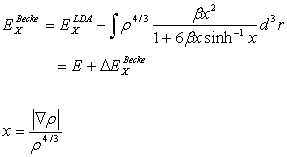 
(2.20)
The parameter ‘b’ can be determined by least-square fit to the
exact Hartree-Fock data, and takes on the value of 0.0042 a.u. The electron density is a function of ‘r’ as
explained earlier. When compared with
the correlation energy obtained through perturbation theory [12], the GGA approach
corrected by the exact exchange behaves extremely well for many atomic and
molecular systems.
2.6 Nudged Elastic Band Method
In chemical kinetics it is often desirable to know the transition
structure, or the energy needed to overcome an energy barrier in a chemical
reaction. It is necessary to
know the reaction path. The Nudged Elastic Band (NEB) method [13-16]
provides a means to determine the minimum energy reaction path and transition
structure in a chemical reaction. The
only three things that one needs to know regarding the reaction are the initial
structure of the reactants, the final structure of the products, and the
interaction potential between atoms in the reaction.
When implementing the NEB method, care must be taken such that the list
of atoms in the initial compounds must be in the same order as the atoms in the
final compounds. That is the atoms of
the initial structure must map to the atoms of the final structure. Care should also be given to the orientation
of the reactants and products. Although
the relative orientation between the initial and final structures does not
affect the results of the calculation, it is easier to view the animation of
the reaction when the relative orientation between the two structures is
similar. The nature of the forces on
the atoms is also a problem. In
semi-empirical approaches, the forces acting on the atoms can be found from the
gradient of the potential energy. In ab-initio
calculations, single point energy and force calculations can be made that are
then used as input to the NEB method [14].
This method was used successfully in the GB study (Chapter 4) and can be
used in further studies where one needs to find reaction paths and transition
structures.
Implementation of the NEB begins by generating a number of
configurations of the reactants called images.
Performing a linear interpolation between the initial structure and
final structure produces these images.
The number of images that need to be generated depends on the
problem. In my problem, the number of
images generated was kept to 20 images or less. An ab-initio force calculation was performed on the atoms in each
image. The atoms of each image were
moved in accordance to the perpendicular component of the force and a parallel
component of a spring force. The
spring force prevented the images from converging on the end points. The sum of the perpendicular component of
the true force and the parallel component of the spring force was used in
calculating the force acting on the atoms in each image. The atoms in the image are moved using a
variant of the Velocity-Verlet method [17].
The steps are repeated until a convergence of the energy and the minimum
energy path is achieved. A C++
subroutine that performs the NEB method in conjunction with the results of
ab-initio calculations is listed in chapter 6.
2.7
Non-linear
Least Square Fit and Optimization
The density functional
hybrid method used in the study of clusters of calcium carbonate molecules
pressed the limits of computational ability rather quickly. I found that the maximum number of CaCO3
molecules that I could perform calculation on in a reasonable time was four
molecules. For cluster systems with
more than four molecules the computational time exceeded 2 weeks. Therefore, it became apparent that if we
were to study the formation of CaCO3 structures with more than four
molecules, other methods had to be used.
The following list gives a benchmark of the time it took to perform
optimizations using the B3PW91/6-311g(d) method on clusters of calcium and
calcium carbonate. Calculations were done
using a SGI workstation (Octane R10000, 225 MHz).
·
Ca8
– 2 days 14 hours
·
Ca13
– 2 - 3 months
·
(CaCO3)1
– 1 hour
·
(CaCO3)4
– 10 days
The RIM potential is a
potential that has been used in the study of CaCO3 lattice
structures [18]. The line of thought now
is to fit the parameters of the RIM potential described in Chapter 5 to the
calculated ab-initio energies and bond lengths of the optimized
structure. A non-linear least square
fit was performed on the two quantities using a combination of the “crude”
method and Newton’s method as described in Chapter 6. To find the best fit to the GGA optimized structure, I minimized
the standard deviation between the optimized GGA interatomic distances and
those of the same structure under the RIM.
The standard deviation was supplemented by that of the optimized
energies as
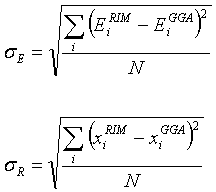(2.21)
where the summation in the first expression is
over the number of optimized structures and the summation in the second
equation is over the number of distances evaluated in the optimized structure
between atom-atom pairs. The
superscript ‘GGA’ refers to the B3PW91/6-311g(d) method. The subscript ‘E’ and ‘R’ refer to the
energy and the positions. Both these s’s were minimized with
respect to the parameters of the RIM potential. Both EiRIM and xiRIM
are the energies and bond lengths of the ab-initio structures but now
calculated with the RIM. Therefore,
these two quantities depend on the 11 parameters of the RIM potential in a
highly non-linear fashion.