In this chapter we perform an exhaustive all-electron
study within the DFT framework and the GGA of calcium clusters containing up to
13 atoms. Results are presented in Section 3.2 for the calcium dimer including
a thorough comparison between various calculation methods. The energetics,
vibrational frequencies, and thermodynamic properties in the harmonic
approximation for Ca3 through Ca13 are
described in Section 3.3. This section
also discusses several isomerization reaction paths and report several cluster
structures corresponding to saddles of the energy surface. A thermally induced structural transition
for Ca12 is highlighted in this section. The study will help us gain insight in to the
models and mechanisms that bring atoms together to form condensed matter.
3.2
Computational Methods
The Kohn-Sham equations [2] were solved self consistently using the GGA representation of the correlation functional. The Becke’s three-parameter hybrid method [7] was used in the study of calcium clusters, as described in Chapter 2. The hybrid method includes the Hartree-Fock exchange and local and non-local terms to the correlation functional provided by Perdew-Wang [9,10]. A triple split valence basis set, 6-311g(d), was used in all calculations involving the calcium atom, i.e. calcium clusters and CaCO3 clusters (see Table 2.1). We found the basis set to be sufficiently large to give good results at a reasonable computational effort. Adding an additional diffuse function produced insignificant changes in both the energy and bond length of Ca2.
Based on the dimer results, all calculations reported in this study of calcium clusters were performed using the triple valence basis set with the addition of a d polarization function. Results in forthcoming sections do not include the Basis Set Superposition Error (BSSE) [35] correction. However, we did test for BSSE with calculations up to Ca4 and found an insignificant decrease in the total energy for these cluster sizes. Worth noting is that BSSE is important when the basis set is small, and our basis set is large.
3.3
Calcium Atom and Dimer
3.3.1 Ionization
Potential
One way to
characterize the various methods and basis sets used in computational chemistry
is to compare the results of the calculations with experiments. Experimental results of the interactions
between calcium atoms are somewhat limited to the ionization potential of the
calcium atom, the dissociation energy of the calcium dimer, and the equilibrium
interatomic distance in the calcium dimer.
Although calcium clusters have been observed in experiments, there is
still a lack of results regarding the properties of calcium clusters. The ionization potential (IP) for the
monatomic calcium is known but the ionization potential (IP) for the calcium
dimer has never been measured or calculated.
The article by Hansen et. al. [36] suggests that the IP for the calcium
dimer should be slightly less then IP for the calcium atom.
The ionization potential for the calcium atom and dimer (the energy required to remove one electron) can be defined by
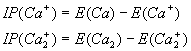 (3.1)
(3.1)
The energy required to remove two electrons is
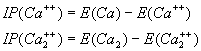 (3.2)
(3.2)
A comparison of different methods was made in the calculation of the ionization potential for both the calcium atom and the calcium dimer. The results of the calculations are summarized in Tables 3.1 and 3.2. For Ca+ we find from the table that the purely density functional method (PW91PW91) gave the best agreement with the experimental value with a percent difference of 0.03%, while the B3PW91 also gave close agreement. The MP4 method had the largest difference with a percent difference of 3.1%. All methods performed well in the calculation of the ionization potentials for the singly ionized calcium.
Table 3.1:
The single and double ionization potentials of the calcium atom using
different methods with the 6-311g(d) basis set.
|
Method |
I ( eV) |
II
(eV) |
|
MP4(sdq) |
5.926 |
17.601 |
|
B3PW91 |
6.006 |
17.883 |
|
PW91PW91 |
6.115 |
18.124 |
|
Experiment |
6.113 |
17.985 |
Table 3.2:
The single and double ionization potential for the calcium dimer using
different methods with the 6-311g(d) basis set.
|
Method |
I
(eV) |
II
(eV) |
|
MP4(sdq) |
5.158 |
14.130 |
|
B3PW91 |
4.950 |
14.068 |
|
PW91PW91 |
4.990 |
14.166 |
For the doubly ionized calcium we have a less then 1% difference for both the B3PW91 and the pure density functional methods (PW91PW91). These are the two methods that performed best overall for both the singly and doubly ionized calcium atom.
3.3.2 Dissociation
Energy
Experimentally the properties of the weakly bonded Ca2 dimer have been extensively investigated [22,36-39]. The results of most interest in this work include the experimental observations by Vidal [22] of the dissociation energy, the equilibrium interatomic distance, and the harmonic frequency.
The binding energy of the calcium dimer is found by determining the difference between the total electronic energy of the calcium dimer and twice the total electronic energy of the calcium atom and a “ghost” atom placed at the same interatomic distance as the calcium dimer. This allowed me to include the Basis Set Superposition Error Correction (BSSEC) in calculations involving the calcium dimer. The equation for the binding energy is
![]() (3.3)
(3.3)
Where Eb is the binding energy, E(Ca) is the quantum mechanical results with one atom and one ghost atom (BSSEC), and E(Ca2) is the quantum mechanical results from the calcium dimer. When the 6-311g(d) basis set was used in the calculation, the BSSEC was found to be small.
Table 3.3
compares previously published results with my results obtained using
B3PW91/6-311g(d). From the table we
can see that my values for the dissociation energy, equilibrium bond distance,
and harmonic frequency agrees well with the experimental values of Vidal
[22]. Many of the previously calculated
results significantly underestimated the dissociation energy. In 1979 Jones [24] used a LDA method to
arrive at a value of 0.2 eV for the dissociation energy, which is higher than
the experimental value of 0.136 eV. The
value I found was 0.144 eV, which is slightly higher than the experimental
value.
Table 3.3:
Summary of energy, vibrational frequency, and equilibriated interatomic
distance for the calcium dimer from my work and previously published results.
|
|
Energy (eV) |
Frequency (cm-1) |
R (Å) |
|
B3PW91/6-311g(d)
This work |
0.144 |
72.29 |
4.269 |
|
NRLMOL |
0.201 |
76.0 |
4.300 |
|
Experimental Vidal
[22] |
0.136 |
65.0 |
4.277 |
|
Experiment Balfour
[37] |
0.133 |
64.93 |
4.28 |
|
Full
CI / [4s2p1d] Pacchioni
[28] |
0.029 |
--------------- |
5.080 |
|
Full
CI / [4s2p] Pacchioni
[26] |
0.007 |
|
6.509 |
|
SCF-LCAO
/ [4s3p] Stoll
[25] |
0.012 |
---------- |
5.503 |
|
DFM
w/ LDA Jones
[24] |
0.20 |
80 |
4.297 |
In the NRLMOL software package we
used 19 non-contracted gaussians augmented by three floating gaussians to
expand each of the ‘s’, ‘p’, and ‘d’ orbitals that were optimized on the
calcium atom.
Since Ca2 is a closed-shell system, it demands a good representation of the electron correlation energy to obtain reasonable total energies. I performed an analysis using different methods on the calcium dimer, which are summarized in Fig. 3.1, where the binding energy (Eb) is displayed as a function of interatomic distance (R). The binding energy is computed as the difference between the total energy of two isolated Calcium atoms (with the BSSE correction) and the total energy of the dimer. The red line shows results using the HF method. The green curve represents the fourth order Moller-Plesset. This method includes single, double, triple, and quadruple substitution (or excitations), abbreviated MP4(SDTQ) [12]. The black curve represents the B3PW91 method. The density functional method, PW91PW91 (magenta), includes a local exchange, given by Slater, the non-local exchange provided by Perdew and Wang91, and the local and non-local correlation functional which are also provided by Perdew and Wang. All calculations were done using Gaussion98 [40]. The accuracy attained in the self-consistent field (SCF) process assures eight decimal places in the energies.
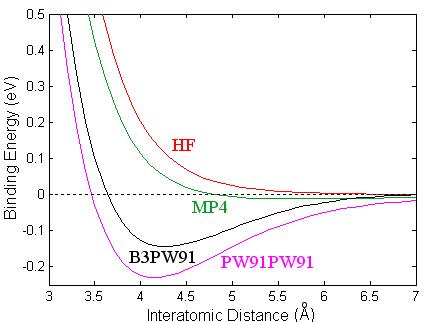
Figure 3.1: Binding energy of Ca2 as a function of interatomic distance using different methods: HF (red), MP4 (green), B3PW91 (black), and density functional PW91PW91 (magenta).
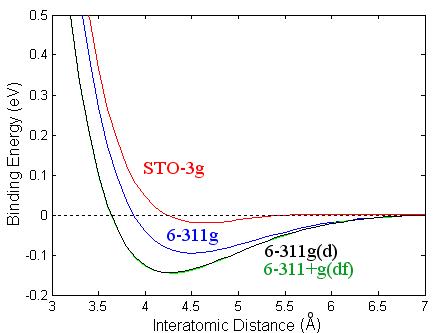
Figure 3.2: Binding energy of Ca2 as a function of interatomic distance using different basis sets: STO-3g (red), 6-311g (blue), 6-311g(d) (black), and 6-311g+g(df) (green).
The same basis set, 6-311g(d) was used in the whole analysis. The HF method is clearly inadequate for describing the calcium dimer since the method results in an unbounded system, and from experiments we know that the system is bounded. That is, the force is purely a repulsive interaction between the two atoms at this level of approximation. It is apparent that the electron correlation will need to be included in any study of calcium systems. In the MP4 calculation the calcium dimer is marginally bounded, having small dissociation energy. This method is inadequate at including the effects of the electron correlation energy resulting in a substantial underestimation of the dissociation energy, while the density functional method overestimates the binding energy. The PW91PW91 results are very close to the early LDA results of Jones [24]. The dissociation energy found with B3PW91 (black line) is 0.144 eV, in good agreement with the experimental results of 0.136 eV [22]. In addition, we found a value of 4.269 Å for the equilibrium bond length, which compares well to the experimental value of 4.277 Å. Our predicted harmonic frequency is 72.3 cm-1, also in good agreement with the experimental results. Such low frequency gives a zero point energy correction to the binding energy of 0.2 kcal/mole. Previous calculations for the dimer have reported significantly different binding energies and interatomic distances.
I have shown that MP4
configuration interaction calculation does not include a large enough set of
configurations to account for the electron correlation energy in the calcium
dimer. The HF description of the electron exchange energy in Ca2 provided by B3PW91 is superior to the functional representation
of that energy in PW91PW91. The agreement between the B3PW91 calculations and
the experimental values of the binding energy, bond distance, and harmonic
frequency for the calcium dimer led us to the hybrid method B3PW91 in our
investigation of larger clusters.![]()
I have also looked at different basis
sets using B3PW91, see Fig. 3.2, and have found that the triple split valence
basis set, 6-311g(d), gave the best result.
A fit of the B3PW91/6-311g(d) energy curve in Fig. 3.3 was made to three potentials; the Lennard-Jones Potential (Eq. 3.4), Mie-Jones Potential (Eq. 3.5), and the Morse potential (Eq. 3.6). The fit was performed over an interval 3.3 to 5.3 Angstroms, which is approximately 1 Angstrom either side of the minimum (4.27 Å). It was felt that this interval would give the best representation in the region of interest.
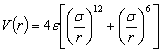 (3.4)
(3.4)
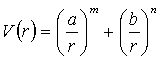 (3.5)
(3.5)
![]() (3.6)
(3.6)
The values for the parameters are listed in Table 3.4 for the three potentials. The parameters for the Morse potential, which gave the best fit to the ab-initio calculation, was found to be De= 0.139140 eV, b=1.093, and r0=4.261 Å, as seen in Table 3.4. The error of the fit was 0.005 eV. The harmonic frequency and anharmonic constant obtained from this Morse potential are we = 68.85 cm-1 and wexe = 1.06 cm-1, respectively. These values are in excellent agreement with those obtained from spectroscopic measurements [22,36,37]. The following was used [41]:
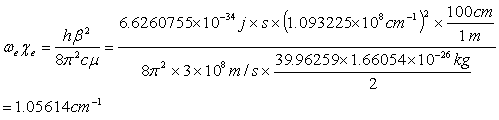 (3.7)
(3.7)
and
![]() (3.8)
(3.8)
From the result of Eq. 3.7 and using Eq. 3.8, the harmonic frequency of the calcium dimer was found to be 68.9 cm-1, which is in good agreement with previously published results of 65 cm-1. Vidal [22] found a value for the Dunham’ coefficient of Y’’20 = 1.081 cm-1. This value is approximately equal to the anharmonic constant and agrees well with my calculation of 1.056 cm-1.
For comparison
purposes, I modeled the results of the binding energy calculations for the
calcium dimer, using the B3PW91/6-311g(d) method and basis set, to various
model potentials. A plot of these model
potentials and my calculated values for the binding energy are shown in Fig.
3.3. The Morse potential (black),
Lennard-Jones potential (Blue) and the Mie-Jones potential (Red) were fitted to
the data points (‘x’ marks) using a non-linear least-square fit.
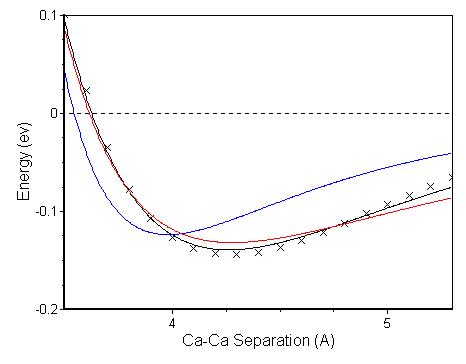
Table 3.4 Optimized parameters to the ab-initio
calculation of the calcium dimer for different model potentials.
|
|
Parameters
|
Standard
Deviation |
|
Lennard-Jones |
e
= 0.123570 eV s
= 3.545893 Å |
0.0416 eV |
|
Mie-Jones |
a=3.374498
Å b
= 3.173516 Å m
= 8.045927 n = 4.262902 |
0.0110 eV |
|
Morse |
b
= 1.093225 Å-1 De = 0.139140 eV r0 = 4.261099 Å |
0.00496 eV |